 Age-structural Models: the Idea
Age-structural Models: the Idea
The age-structural domain is the unifying feature of Age Structural Theory. Rather than consider relationships over chronological time, age-structural models re-position state behaviors on the age-structural domain—an X-axis that follows the continuous path of the age-structural transition, situating it as the principal independent variable. The age-structural domain, measured in median age, is the only continuous independent variable in logistic regression analysis. All controls and treatment variables are dichotomous (0,1). Likewise, the functional forms that are fitted to data by logistic regression are displayed across a domain beginning at a median age of 15 years and ending at 55 years.
Each age-structural model begins as a hypothesis, whether generated notionally (from theory) or observationally, that a measurable state behavior is typically associated with the movement of states through the age-structural transition. It is important to stress—and periodically re-iterate—that these models begin as a hypothesis that is epistemologically situated at the very edge of Age-structural Theory. Some age-structural models have been strengthened and brought into the more certain body of theory by repeated in-sample testing, out-of-sample testing, and some form of successful prediction. A few others—particularly hypotheses associated with the age-structural model of liberal democracy (ASM-LD)—have demonstrated their utility by out-competing other methods of analysis and by exposing original insights into the processes under study.
In my analyses, age-structural models employ the country-level median age as the only continuous independent variable. In these analyses, logistic regression has been used to determine (1.) whether, or not, the presence of a specific, discrete condition (the dependent variable) varies as states advance across the age-structural transition. If, indeed, it varies across this transition, then (2.) age-structural methods proceed to determine how that specific condition varies (its functional form); and (3.) the level of certainty that is associated with that variation (its confidence interval).
In age-structural models, the dependent variable (composed of data coded “1” or “0”) must be discrete, or discretized by creating a gradient of discrete categories. Examples of discrete conditions include the presence or absence (in a year) of a type of political regime, or the presence or absence of an intra-state conflict. Examples of discretized variable include the attainment of specific levels of per-capita income (e.g., the World Bank’s Upper-middle Income Category), or levels of educational attainment (secondary school participation).
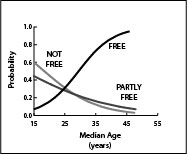
For logistic regression to produce a reasonable fit to these data, the frequency of the dependent variable, as it is sampled across the age-structural domain, must be adequately described by a logistic function—a monotonic sigmoid curve generated by the Verhulst equation (an S-shaped function, beginning low and approaching an upper asymptote), or to some segment of a logistic curve (Maynard, 2001). Therefore, a segment of a logistic function can neither be fit adequately to frequency data that (a.) rises substantially and then falls, nor (b.) falls substantially and then rises again across the domain.
Age-structural Theory is a reductionist project. Operating on a single, continuous X-axis simplifies statistical analyses and permits the visual display of relationships on a two-dimensional graph. And, like all simplified statistical theories, it has limitations. Firstly, it suffers from the “small number problem”—predictions are most successful when considering clusters of states, rather than betting on a single state. Secondly, by itself, taking only median age into account, age-structural models are blind to the influence of non-demographic and sub-national demographic factors. Unless these are noted through observation, studied through separate analyses, or added experimentally as discrete (0,1) variables to the statistical analysis, its reliance on the country-level scalar measure of median age as the lone continuous domain of its analysis can obscure important factors. For example, observations of the functional form of the age-structural model of liberal democracy have shown that presence of a small population size (under 5 million) and regime types have substantial impact on outcomes (Cincotta, 2015a, 2015b; Weber, 2013).
In its classic form (which was used to describe constrained population growth), the logistic function begins at its lowest point, accelerates to an inflection point, decelerates, and then levels off as it approaches an upper asymptote. However, this function can also be parameterized to operate in reverse: to begin at its high point and descend to a lower asymptote. Upward or downward sections of the function can be fit to data, as well.
